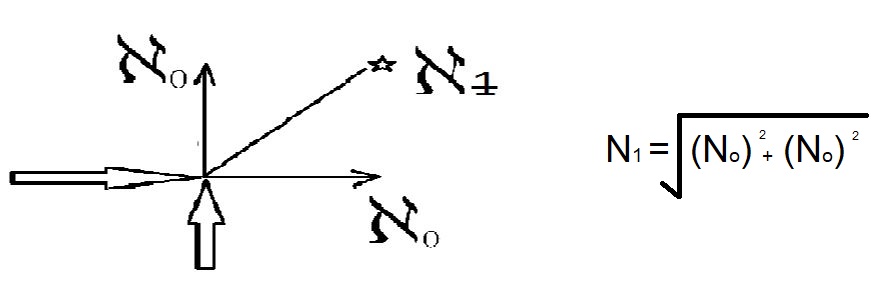
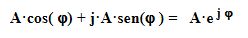Nei vari studi relativi al “principio d’indeterminazione”, in meccanica quantistica, si stabiliscono i limiti nella misurazione dei valori di grandezze fisiche coniugate, nella forma più nota, il principio di indeterminazione viene espresso dalla relazione:
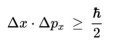
fra l’incertezza sulla posizione
spaziale “Dx” e quella sulla quantità di moto “DPx”
di una particella, dove “h” è la costante di Planck
ridotta (o costante di Dirac, valore sperimentale equivalente a
1,0545…E-34 J*s).
Enunciato nel 1927 da Werner Karl
Heisenberg e confermato da innumerevoli esperimenti, rappresenta un
concetto cardine della meccanica quantistica e sancisce una radicale
rottura rispetto alle leggi della meccanica classica.
Ulteriori evoluzioni teorico pratiche
del principio di indeterminazione sono state condotte da vari
scienziati con l’utilizzo di formule complesse e l’utilizzo di
“dispositivi numerici” sempre più raffinati.
Io credo che l’impiego di un concetto di numero universale, possa essere giustamente rappresentato nelle sue componenti naturali e immaginarie, e che solo in questo modo si possano utilizzare per esprimere correttamente la rappresentazione energetico esistenziale della materia.
Vorrei chiarire il concetto partendo da
questi presupposti elementari:
- il genere umano per comunicare
effettua delle “categorizzazioni mentali” esprimendo tali
operazioni tramite concetti più o meno complessi. - Nell’ambito delle categorizzazioni
mentali, quelle che riguardano il concetto di relazioni numeriche,
sono sicuramente quelle che impegnano moltissimo le facoltà mentali
e che nel tempo sono state soggette a trasformazioni sempre più
complesse. - L’approccio mentale per
comprendere le relazioni dei concetti nel campo delle
categorizzazioni numeriche ha sviluppato linguaggi sempre più
“coerenti” sotto l’aspetto funzionale: l’ambito LOGICO.
Partendo dal concetto primordiale di numeri naturali si sono definiti dei simboli per identificare delle quantitÃ: “N” → (0… 1… 2… 3… 4 … 5… 6… 7… 8… 9…) (simbologia moderna ma di antica origine indiana).
Le relazioni interattive di carattere pratico, quali combinazioni utilizzanti i concetti numerici di cui sopra hanno permesso di concepire operazioni elementari di somma, sottrazione dando origine alla estensione “intuitiva” di questa tipologia di categorizzazione mentale introducendo la definizione dei numeri interi relativi: “Z” → (… -3… -2… -1… 0 … 1… 2… 3… …) che comprendono i “numeri negativi”
Dalle necessità pratiche,
probabilmente dovute a esigenze di spartizione dei beni vennero
introdotti i concetti di divisione e moltiplicazione, portato alla
categorizzazione ancora adesso definita come “insieme dei numeri
razionali”, anche se a mio parere la parola “razionale” non è
del tutto adeguata, perlomeno in italiano.
La rappresentazione dei numeri
razionali è la seguente:
“Q” → (… -(Nx/Nx)… -(Nx/Ny) …
(Nx/Nx)… (Ny/Nx) … ) → (…-1/2 … -1/3 … 1/2 … 1/3 …)
tali numeri solitamente sono anche
rappresentabili in questo modo:
… -1.0… -0.9999… -0.5…. 0.0 … 0.5… 0.75555… 1.0… …. (come separatore decimale si può usare ance la virgola “,”….. 😉
(nota: si passa dalle categorizzazioni mentali alle convenzioni sociali…)
che però può implicare qualche difficoltà interpretativa nei casi in cui venga considerato anche il numero “0” → ( 0/Nx …. Nx/0 …) questa particolarità ha portato alla concettualizzazione elementare di infinito: ……………………………………………………….“Ꝏ”……………………………………………………..
Dalle esigenze dovute alle misurazioni spaziali invece, le categorizzazioni mentali relative all’utilizzo della simbologia hanno fatto in modo di dover introdurre il concetto dei “numeri algebrici”, basti pensare alle applicazioni della “Geometria Euclieda” ed in particolare al teorema di Pitagora, dove una variante dell’enunciato recita: “La misura dell’ipotenusa è data dalla “radice quadrata” della misura dei cateti…”, per noi occidentali, anche se questi enunciati erano noti anche ad altre culture…. perlomeno in oriente.
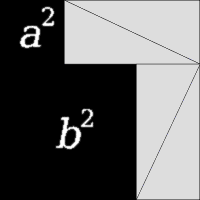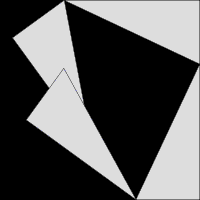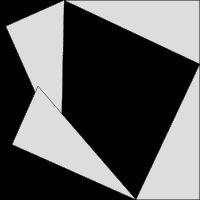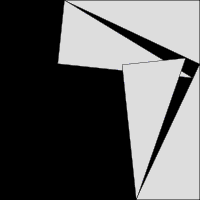
In particolare, la condizione che
probabilmente portò Ippaso al concetto dei “numeri irrazionali”
e che sono esprimibili come “radici” di equazioni algebriche:
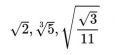
in altre parole numeri non esprimibili
correttamente se usassimo una delle versioni precedenti:
√2 =1,4142135623730950488016887242097… (e non può essere il risultato di una frazione)…
da questa categorizzazione di numeri si
può dedurre un altro concetto interessante:
dati come valori infiniti quelli
rappresentati da No, il valore rappresentato da N1
è sicuramente maggiore: un infinito più
grande…. (fare riferimento al valore della
radice quadrata)
Ulteriori esigenze di misurazione, in
particolare dovute a procedure di misurazioni orografiche o che in
qualche modo comprendessero misure di curve portarono alla
categorizzazione dei numeri trascendenti, quali “ Л“
ed “e”, il primo come sappiamo viene definito come l’area
di un cerchio di raggio “1”, mentre il secondo viene definito
come risultato di una serie infinita di frazioni di numeri
fattoriali:
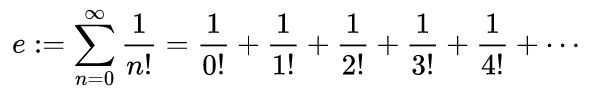
Ecco allora l’esigenza di far
“rientrare” tutte queste tipologie di numeri in una categoria
mentale che li rappresentasse: l’insieme dei numeri reali “R”,
che comprende i numeri esprimibili con o senza virgola (decimali),
quindi i numeri “razionali”, e quelli “irrazionali”,
algebrici e trascendenti.
Attraverso questi numeri si possono
esprimere le grandezze scalari (quantità di cose…) o determinare
delle istantanee di grandezze vettoriali (forze, velocità ecc) ,
tuttavia si resero necessarie ulteriori categorizzazioni mentali per
esprimere dei concetti in grado di esprimere dei vettori variabili
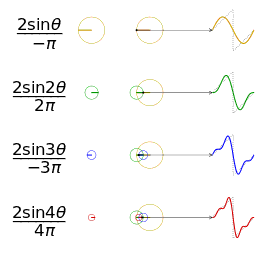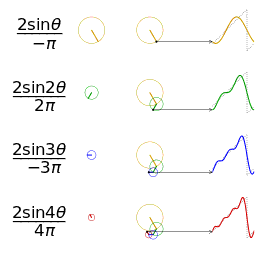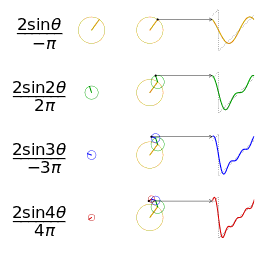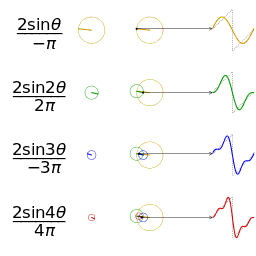
nel tempo (vettori rotanti.. onde sinusoidali…):
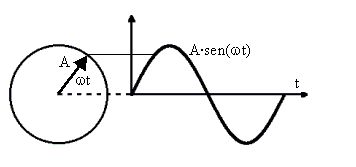
->
rappresentazione di numeri complessi:
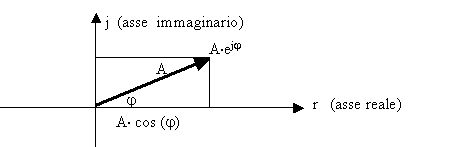
I=X+JY
dove “J” è semplicemente un rotore
immaginario che farà in modo di ottenere un particolare risultato:
J2 = -1
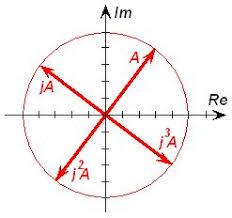
Ecco allora
che tutte le categorizzazioni precedenti, ancora una volta verranno
“incluse” in un nuovo “insieme numerico”, che tradotto nel
sistema di comunicazione coerente dovuto al linguaggio matematico si
traduce in:
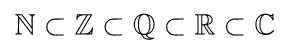
da quanto
sopra si può desumere che nelle categorizzazioni mentali quella che
contempla tutti gli altri numeri sia appunto quella dei numeri
complessi.
Ma il genere
umano evidentemente fa buon uso della fantasia e quindi alcuni
“addetti ai lavori”, per particolari esigenze, hanno introdotto
delle ulteriori concettualizzazioni nel campo dei numeri complessi,
definendo i “Quaternioni”(usati anche in robotica), gli
“Ottonioni”, gli “Sedenioni”, nonosolo, nel campo dei numeri
reali sono stati introdotti concetti come i “numeri iperreali”,
numeri “non standard” che fungono da base per l’analisi
matematica moderna nel calcolo delle derivate e degli integrali.
La loro
forma descrittiva è la seguente:
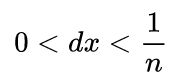
dato come assunto che vi sia un numero dx compreso tra “0” ed un valore “1/n”, il numero iperreale si può scrivere come “ X+dx” ovvero “X + ɛ”. o “monade” → “μ(x)”.
Non solo, ma
sono stati definiti concettualmente anche i cosiddetti numeri
“p-adici” che assumono la seguente formula di rappresentazione
nel linguaggio matematico:
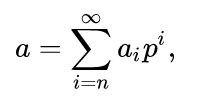
che ad
esempio (10-adici) si potrebbero rappresentare come una somma
infinita di interi a sinistra della virgola come riportato dalla
seguente:
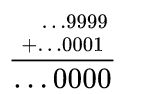
Nella forma 10_adica quindi …99999 = -1.
Questa tipologia di categorizzazione numerica venne introdotta probabilmente per effettuare operazioni complesse in analisi matematica delle metriche.
Quanto sopra
descritto porta nella direzione della categorizzazione
“numerologica” quale approccio di analisi dei fenomeni fisici,
dove possiamo indicare semplicisticamente che i “numeri”, con le
loro relazioni funzionali, stanno alla base di un linguaggio logico,
quindi coerente, in grado generare dei modelli atti ad interpretare
quella che riteniamo essere la realtà fenomenologica dell’universo.
Alcuni
esempi:
Il peso è una forza, ha una unità di misura numerica e si può rappresentare con un vettore (non rotante):
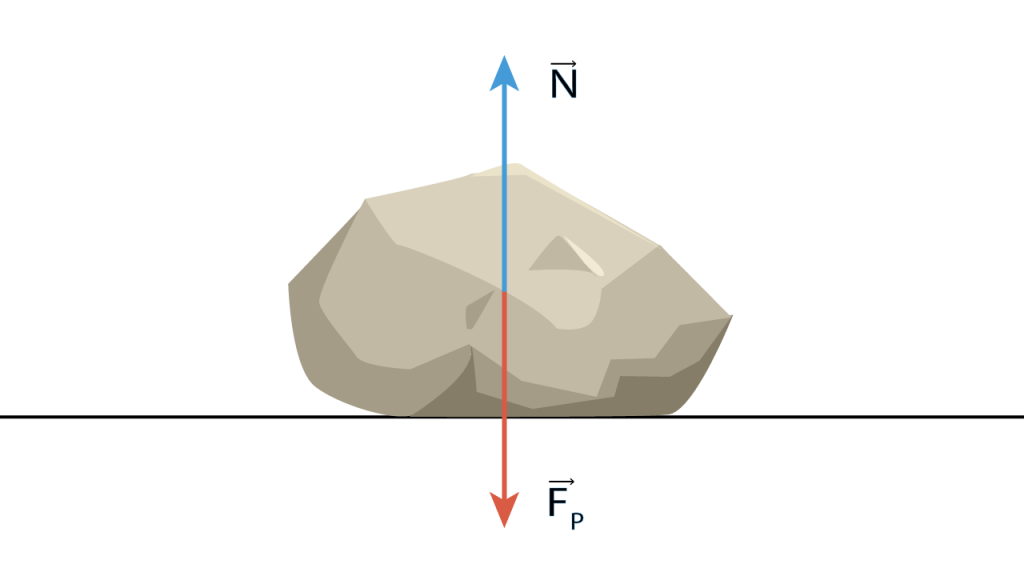
La massa invece esprime una quantità di materia, ha una unità di misura ed è una grandezza scalare:

siccome un atomo d’oro ha una massa pari a 3.2707068*10-22g presumibilmente ci vorranno circa un numero pari a 3,05744311902247E+018 atomi di oro (senza scorie di altri materiali) 😉
A proposito
di numeri, quando questi vengono utilizzati per rappresentare
qualcosa nel mondo geometrico, trasferiscono, come è intuibile
alcune delle loro proprietà ad alcuni elementi, per il calcolo di
aree, di lunghezze di archi ecc.
Esistono
diversi tipi di geometrie, alcune anche molto complesse e
apparentemente paradossali e di difficile comprensione.
A me piace
immaginare la geometria come un metodo di rappresentazione verosimile
della realtà fisica degli elementi e ad esempio se mi riferisco ad
un punto, che concettualmente non ha dimensioni, se lo riporto su una
geometria piana cerco di immaginare un cerchio con un diametro nullo
(ma sempre un cerchio), e quindi se devo immaginare un segmento
immagino una serie infinita di cerchi, uno accanto all’altro… (ma
un infinito determinato dai confini del segmento), se dovessi
immaginare una linea sarebbe una serie infinita di punti senza
limiti, se dovesse essere un piano lo vedrei come cerchi disposti su
un area e così via perlomeno fino ad immaginare dei solidi.
E’ importante inoltre, assumere come concetto di base delle geometrie, che si deve fare sempre riferimento ad un sistema di coordinate, ad esempio, nella geometria piana si definiscono le ascisse e le ordinate (le coordinate “cartesiane” introdotte concettualmente da Cartesio).
Ora,
prendiamo in considerazione un punto e associamolo ad una coordinata,
in qualsiasi direzione spaziale… potrebbe anche essere interpretato
come una linea:
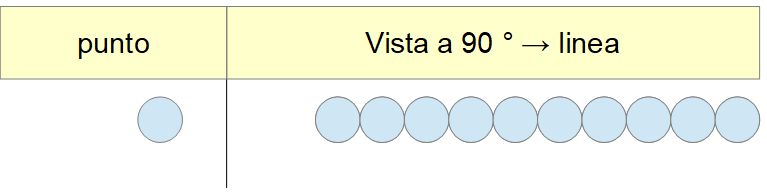
Se aggiungiamo un’altra coordinata potremmo vedere un piano:
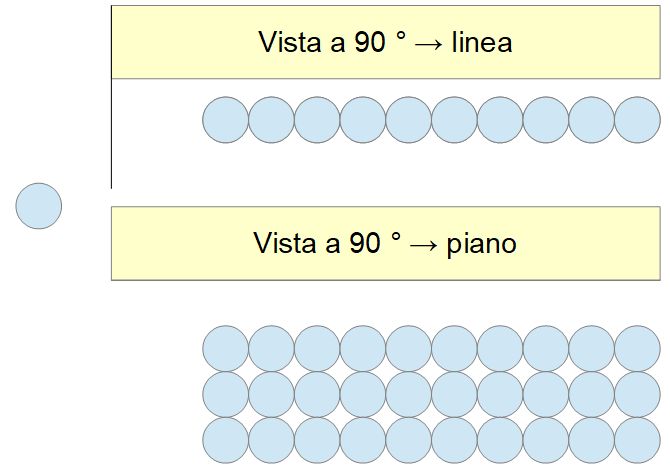
Se aggiungessimo un’altra coordinata scopriremmo un solido:
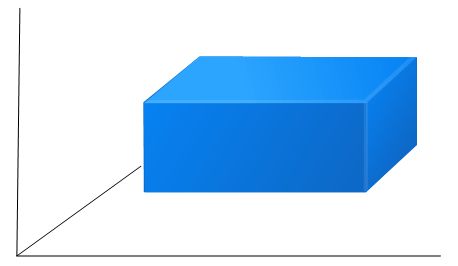
Con un po’
di immaginazione i numeri “razionali” potrebbero essere associati
a dei cerchi…
e i numeri iperreali come dei cerchi più piccoli…
Nella geometria solida potremmo immaginare i numeri come delle sfere, magari introducendo i numeri immaginari e fornendo un concetto di “propagazione d’onda”, se non proprio i quaternioni…
Questi sono i “ferri del mestiere” per chi si appresta ad entrare nel mondo della automazione e della robotica.